CS 4495 / 6476 Project 3: Camera Calibration and Fundamental Matrix Estimation with RANSAC

Matching based on Fundamental Matrix
Overview
The objective of this project is to apply the knowledge of camera and scene geometry. In general, the project consists of three parts: The first part is to estimate the camera projection matrix which maps the 3D coordinates (real world) to 2D coordinates (image), and thus find the camera center of the view. The second part is to estimate the fundamental matrix based on the input 2D point pairs. The final part is to estimate the fundamental matrix using the RANSAC based on the unreliable point pairs given by SIFT matches.
- Estimate the Projection Matrix and Camera Center
- Estimate the Fundamental Matrix based on Point Pairs
- Estimate the best Fundamental Matrix using RANSAC
- Extra: Normalization
Estimate the Projection Matrix and Camera Center
The projection matrix is a linear transformation which aims to convert the real world 3D points to image 2D points. To estimate the projection matrix is to solve the M using linear algebra on the given point pairs. The homogeneous coordinates of the equation for moving from 3D world to 2D camera coordinates is shown below:
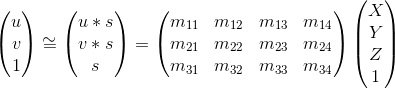
To fix the scale for the matrix, I set the last term in the matrix, which is m_34, as 1. Then I solve the matrix based on the given point pairs. After I get the matrix, I simply computed the camera center using the formular: 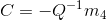 . The results of part one is shown below.
. The results of part one is shown below.
Table 1: Projection Matrix and Camera Center Evaluation
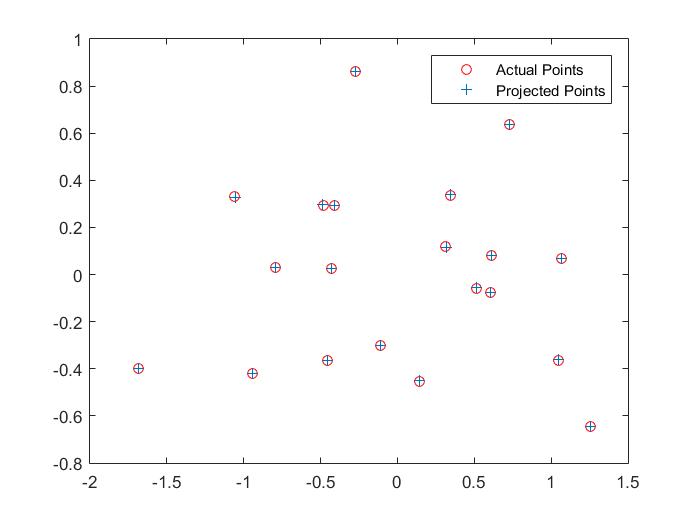 |
 |
| Point Pairs 1: Projection Matrix Evaluation 2D | Point Pairs 1: Projection Matrix Evaluation 3D and Camera Center |
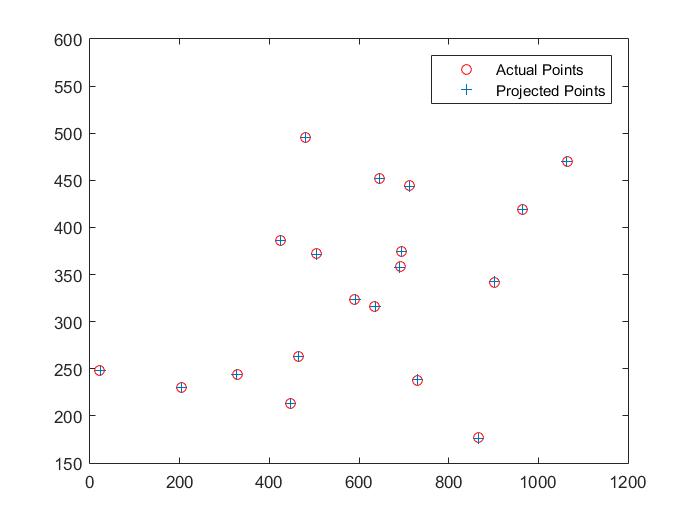 |
 |
| Point Pairs 2: Projection Matrix Evaluation 2D | Point Pairs 2: Projection Matrix Evaluation 3D and Camera Center |
Estimate the Fundamental Matrix based on Point Pairs
Like part one, part two is to estimate the fundamental matrix, which is a linear transformation between 2 images, both 2D points. The homogeneous coordinates of the equation for moving from 3D world to 2D camera coordinates is shown below:
Similarly I set the last term as 1 to fix the scale, and then we only need 8 pairs to solve the matrix since we only have 8 unknowns. After solving the matrix, I need to set the least singular value in Σ to zero thus generating Σ2. The results of part two is shown below.
Table 2: Fundamental Matrix Estimation
 |
 |
| Image No.1 | Image No.2 |
Estimate the best Fundamental Matrix using RANSAC
The final part is to find the best fundamental matrix using the RANSAC based on the unreliable point pairs given by SIFT matches. I interatively pick a mount of points as a sample and calculate the fundamental matrix of the sample and apply the matrix on all points. I set a threshold as the criteria. Any points with the distance from the expected value drived from fundamentall matrix are considered as inliers, and others are outliers. The best matrix is the one has the most inliers compared with other matrices. Using the best estimation, I find 30 pairs with the greatest confidence and show them on the images. The results are shown below, the parallel matchings are reliable while the others are most incorrect.
Table 3: Matching Results Using the most confident Fundamental Matrix
 |
 |
| Mount Rushmore IMG 1 | Mount Rushmore IMG 2 |
 |
| Confident Matching (80% accuracy) |
Extra: Normalization
The results can be improved by normalize the coordinates of the points before solve the fundamental matrix. I pick the square root of 2 as STD and adjust the points based on center (the mean of the points) and the standard deviation ratio. The basic formulaof the normalization is shown below:
% Code for Normalization
% normalization matrix
S_a = diag([1, 1, 1]);
S_b = diag([1, 1, 1]);
C_a = diag([1, 1, 1]);
C_b = diag([1, 1, 1]);
ca = mean(Points_a);
cb = mean(Points_b);
C_a(7: 8) = -ca(1 : 2);
C_b(7: 8) = -cb(1 : 2);
std_cof = 2 ^ (0.5);
std_a = std(Points_a(:,1) - ca(1)) + std(Points_a(:,2) - ca(2));
std_b = std(Points_b(:,1) - cb(1)) + std(Points_b(:,2) - cb(2));
sa = std_cof / std_a;
sb = std_cof / std_b;
S_a(1) = sa;
S_a(5) = sa;
S_b(1) = sb;
S_b(5) = sb;
T_a = S_a * C_a;
T_b = S_b * C_b;
Points_a(:, 3) = 1;
Points_b(:, 3) = 1;
% normalize the points
Points_a = T_a * Points_a';
Points_a = Points_a';
Points_b = T_b * Points_b';
Points_b = Points_b';
...
% normalize the fundamental matrix
F_matrix = T_b' * F_matrix * T_a;
After normalization, the results are better the original ones. Results of part two are slightly improved while the results of part are much better.
Table 4: Results with Normalization (Part two)
 |
 |
| Image No.1 without Normalization | Image No.1 with Normalization |
 |
 |
| Image No.2 without Normalization | Image No.2 with Normalization |
Table 4: Results with Normalization (Part three)
 |
| Mount Rushmore Matching without Normalization |
 |
| Mount Rushmore Matching without Normalization |
 |
| Notre Dame Matching without Normalization |
 |
| Notre Dame Matching without Normalization |
 |
| Episcopal Gaudi Matching without Normalization |
 |
| Episcopal Gaudi Matching without Normalization |